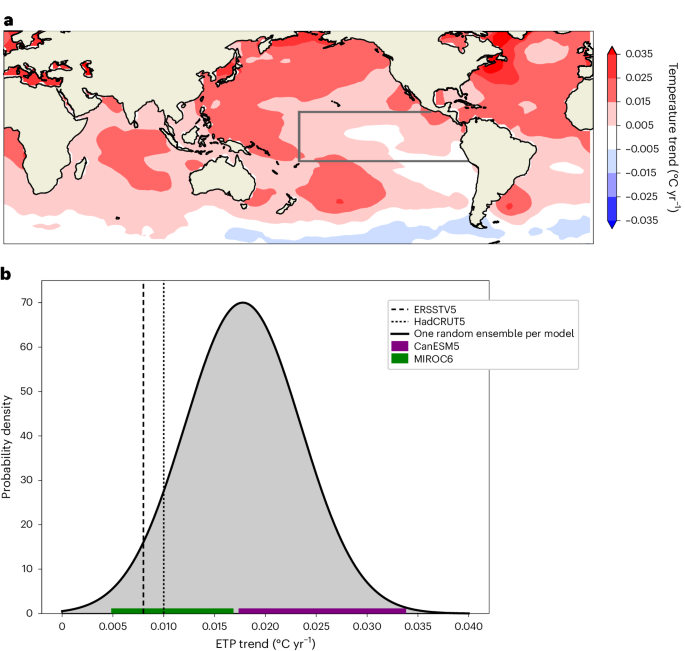
Model data and observation
This study uses simulations of GSAT change in 2081–2100 relative to 1995–2014, from CMIP6 model simulations driven by both SSP5-8.5 and SSP1-2.6 scenarios16,43. We use the historical GSAT trend over the period 1970–2022 as a predictor. The historical period 1970–2022 is used for calculating the past warming trend because the correlation with projected warming is highest for trends calculated over this period (outlined in ‘The optimal time period of past trends for constraint’). This is probably because the GSAT trend response to aerosol changes over this period is relatively small compared with other longer periods so that the dominant external forcing is greenhouse gases, as in the future3. In addition, the 53-year 1970–2022 period reduces the influence of decadal to multi-decadal internal variability relative to the use of shorter periods. The CMIP6 model simulations used to calculate the GSAT trend (based on near-surface air temperature) and ETP trend (based on SST) are listed in Supplementary Table 1. The corresponding observed GSAT trends are derived from HadCRUT544, Berkeley Earth45 and NOAAGlobalTempv546, while observed ETP trends are derived from HadCRUT544 and Extended Reconstructed Sea Surface Temperature version 5 (ERSSTv5)47.
Estimating the impact of ETP variability on the GSAT trend
We construct a linear regression model of the relationship between the GSAT trend and ETP trend using pre-industrial control simulations from each climate model. We extract the last 477 years of the control simulation of each model and divide this into nine 53-year segments. We calculate a regression coefficient using nine ensemble member per model and bootstrap with replacement 5,000 times to calculate uncertainties (Fig. 2a). We also check our results by carrying out a similar analysis using a 53-year period from the historical simulation with minimal trends in radiative forcing (1850–1902).
Removing ETP-congruent variability in the GSAT trend
We use two steps to remove the internal variability in the GSAT trend that is congruent with variations in ETP SST trends. The first step is to estimate unforced internal variability over the ETP region for the set of model realizations. As shown in Extended Data Fig. 3, the forced component of the ETP trend, estimated as the ensemble mean for each model, is moderately correlated with the equilibrium climate sensitivity (ECS) across CMIP6 models (r = 0.64, P < 0.01; Extended Data Fig. 3). This connection indicates that part of the multi-model variance of the ETP trend can be explained by model differences in forced response.
In particular, a regression model based on the individual models’ ensemble means of ETP trend from historical simulations (denoted as \(\bar{{\bf{A}}{\boldsymbol{}}\,}\), with the overbar representing averaging over initial condition ensembles for an individual model) and modelled ECS (\({\bf{B}}\)) can be established (equation (1)), where \({\alpha }_{1}\) is the intercept and \({{\bf{\upbeta }}}_{{\boldsymbol{1}}}\) is the regression slope; \({{\boldsymbol{\varepsilon }}}_{{\boldsymbol{1}}}\) represents the regression residuals. The number of rows in \(\bar{{\bf{A}}}\) and \({\bf{B}}\) is equal to the number M of climate models used.
$$\bar{{\bf{A}}}={\alpha }_{1}+{{\bf{\upbeta }}}_{{\bf{1}}}{\bf{B}}+{{\bf{\varepsilon }}}_{{\bf{1}}}.$$
(1)
The unforced ETP trend (\({{\bf{A}}}^{{\boldsymbol{(}}{\boldsymbol{1}}{\boldsymbol{)}}}\); shown on the x axis of Extended Data Fig. 1) over 1970–2022 from the historical experiment is estimated by subtracting the forced ETP trend for each model \(\bar{{\bf{A}}}\) from ETP trends of individual realizations from that for model \({\bf{A}}\) thus
$${{\bf{A}}}^{({\bf{1}})}={\bf{A}}-{\alpha }_{1}-{{\bf{\upbeta }}}_{{\bf{1}}}{\bf{B}}.$$
(2)
In the second step, we remove the unforced ETP-congruent internal variability from the GSAT trend in the observations, as well as in each model simulation. We assume that the impact of ETP variability on the GSAT trend in the multi-model CMIP6 ensemble is exchangeable with the real world. This removal is based on the regression relationship established using the pre-industrial control simulations (Fig. 2).
Specifically, the regression coefficient, \({{\bf{\upbeta }}}_{{\boldsymbol{2}}}\), of unforced GSAT trend variations (\({\bf{C}}\)) against unforced ETP trend variations (\({{\bf{A}}}^{{\boldsymbol{(}}{\boldsymbol{2}}{\boldsymbol{)}}}\)) is estimated from the pre-industrial control based on regression equation (3), where \({{\boldsymbol{\varepsilon }}}_{{\boldsymbol{2}}}\) represents the regression residuals, as
$${\bf{C}}={{{\bf{\upbeta }}}_{{\bf{2}}}{\bf{A}}}^{({\bf{2}})}+{{\boldsymbol{\varepsilon }}}_{{\bf{2}}}.$$
(3)
The number of rows in \({\bf{C}}\) and \({{\bf{A}}}^{{\boldsymbol{(}}{\boldsymbol{2}}{\boldsymbol{)}}}\) is equal to M times nine (as the control integrations are separated into nine sections). Then, for the historical GSAT trend in 1970–2022, the unforced ETP-congruent variability in GSAT trend (\({{\bf{C}}}^{{\boldsymbol{(}}{\boldsymbol{1}}{\boldsymbol{)}}}\)) can be estimated by equation (4) as
$${{\bf{C}}}^{({\bf{1}})}={{{\bf{\upbeta }}}_{{\bf{2}}}{\bf{A}}}^{({\bf{1}})}.$$
(4)
Finally, the historical GSAT trend over the period 1970–2022 (x) is used with the ETP-congruent variability (\({{\bf{C}}}^{{\boldsymbol{(}}{\mathbf{1}}{\boldsymbol{)}}}\)) to estimate the GSAT trend without ETP-congruent variability (\({{\bf{x}}}^{{{{\prime} }}}\)) as
$${{\bf{x}}}^{{\prime} }={\bf{x}}-{{\bf{C}}}^{({\bf{1}})}.$$
(5)
We estimate the observed unforced ETP trend (the ERSSTv5 and HadCRUT5 are two observation datasets used to calculate the ETP trend) based on equations (1) and (2) by sampling from a Gaussian distribution fitted to the assessed very likely range of ECS (with a mean equal to the AR6 best estimate 3 °C and a standard deviation of 0.6°C). A range of observed GSAT trends with unforced ETP-congruent variability removed is then estimated using equations (4) and (5). We account for observational uncertainty by sampling the GSAT trend from three datasets (HadCRUT5, Berkeley Earth and NOAAGlobalTempv5) and sampling the ETP trend from two observed ETP datasets (HadCRUT544 and ERSSTv547). The sampling process described here is coordinated with sampling strategies addressing internal variability in observational constrained projections (outlined below).
Regression model for observational constraint
The constrained projections are obtained using linear regression as described below. We first apply ordinary least-squares regression to fit the linear model \({\bf{y}}=\alpha +{{\bf{x}}}^{{\intercal}}{\bf{\upbeta }}\). The historical predictor is denoted by \({\bf{x}}\) and future predictand is represented by y. The number of rows in \({\bf{x}}\) and y is equal to the number M of climate models used. By introducing an observational estimate \({{\bf{x}}}_{{\bf{0}}}\) of the predictor into the linear regression model, the best estimate of projected warming due to the constraint is denoted by \({\hat{y}}_{0}\). Assuming Gaussian regression errors, the constrained projection has the PDF48,49,50
$$p\left(\left.y\right|{{\bf{x}}}_{{\bf{0}}}\right)=\frac{1}{\sqrt{{2\pi \sigma }_{{\hat{y}}_{0}}^{\,2}}}\exp \left(-\frac{{\left(y-{\hat{y}}_{0}\right)}^{2}}{2\,{\sigma }_{{\hat{y}}_{0}}^{2}}\right),$$
(6)
where
$${\sigma }_{{\hat{y}}_{0}}^{2}{=s}^{2}\left(1+{{\bf{x}}}_{{\bf{0}}}^{{\intercal}}{({{\bf{x}}}^{{\intercal}}{\bf{x}})}{\,}^{-1}{{\bf{x}}}_{{\bf{0}}}\right)$$
(7)
and
$${s}^{2}=\frac{1}{M-2}\mathop{\sum }\limits_{m=1}^{M}{\left(\;{y}_{m}-{\hat{y}}_{m}\right)}^{2}.$$
(8)
Sampling strategies to account for internal variability
To account for the influence of internal variability, we derive our constrained projections by randomly selecting one ensemble member from each model (see Extended Data Fig. 4 for the schematic plot). We repeat this random selection process 5,000 times during the imperfect model test evaluation and observational constraint procedure. This approach serves two purposes: it mitigates the influence of substantial variations in the ensemble size across different models and enables us to estimate the impact of internal variability in the model simulations on our constrained projections. Additionally, we conduct a sensitivity test to evaluate whether our constrained results are biased by the limited number of models with ensemble sizes larger than one. To account for the contribution of observational uncertainty to the constrained uncertainty, we randomly sample over GSAT and ETP SST observational datasets while sampling over internal variability.
Imperfect model test
To assess the constraint’s performance we apply a cross-validated imperfect model test3,6, in which simulations from each model serve in turn as pseudo-observations and are used to constrain projections by all other models (see Extended Data Fig. 5 for the schematic plot). The evaluation is based on values of the r.m.s.e. and correlation coefficient, both calculated using the pseudo-observations and the means of the constrained imperfect model ensemble. We examine what fraction of pseudo‐observations lie within the 5–95% constrained uncertainty range for each projection, across all models, to assess the coverage probability3,6. Ideally, 90% of the pseudo‐observations would lie in the constrained 5–95% uncertainty range in this test. To ensure a fair assessment of predictor performance comparable with observations, instead of using the known ECS for each model to calculate the forced component of its ETP trend, we instead sample ECS from a Gaussian distribution centred on the ECS of each model, with a standard deviation taken from the AR6-assessed likely ECS range. This allows for the generation of a pseudo-observed GSAT trend with ETP-congruent variability removed with appropriate uncertainties.
The optimal time period of past trends for constraint
To determine the optimal time period to minimize the influence of internal variability and maximize the strength of the statistical relationship between past trends and future warming in the CMIP6 models, we vary the date range over which trends are calculated. We calculate the r between historical trends (based on different start and end years) and projected warming between 1995–2014 and 2081–2100 under SSP5-8.5 across CMIP6 models. In this calculation, we consider the first ensemble member of each model. The corresponding results are shown in Extended Data Fig. 9.
As shown in Extended Data Fig. 9a, holding the end year close to the present (for example 2014 or 2022) and making the start year later than the 1970s results in progressively weaker correlation coefficients, due to the increasing influence of internal variability. Probably as the uncertain GSAT response to aerosols is relatively constant over this period2,3, the GSAT trend from the 1970s to the present is better correlated with future projected warming compared with periods with earlier start dates (for example, 1850–2022). As shown in Extended Data Fig. 9b,c, by reducing the internal variability, removing the ETP-congruent part of the GSAT trend results in a stronger correlation coefficient with projected warming, especially for GSAT trends calculated over a relatively short period (for example, 1999–2014, 1999–2022 and 2014–2022).
The periods over which the GSAT trend with ETP variability removed exhibits the highest correlation with projected warming are 1970–2022 (with r = 0.82), 1984–2014 (r = 0.83), 1984–2022 (r = 0.81) and 1999–2022 (r = 0.81). These periods all show a strong correlation between past trends and future changes across models. Considering that a longer period is expected to reduce the influence of internal variability (and we note that results shown in Extended Data Fig. 9 are based on a single ensemble member), we, therefore, choose 1970–2022 as the best period to constrain future warming.
Justifying PDF averaging for final constrained uncertainty
As described above, our study samples over initial condition ensembles from climate models, using one ensemble member per model. Each sample gives us a distribution of projected GSAT change (y in equation (9)), with a particular mean (μ) and standard deviation (σ). Hence, multiplying the joint distribution of these two statistics f(μ, σ), by a conditional distribution f(y | μ, σ), and then integrating over μ and σ gives us a population estimate p(y) of the marginal PDF of projected GSAT changes
$$p\left(\;y\right)=\iint f\left(\left.y\right|\mu ,\sigma \right)f\left(\;\mu ,\sigma \right){\rm{d}}\mu {\rm{d}}\sigma.$$
(9)
Based on our sampling strategy, each derived PDF with its corresponding value of μ and σ is equally probable. Sampling μ and σ from their joint distribution and then averaging the resulting conditional distributions hence gives a sample estimate of this population mean distribution of \(y\).
Synthetic test on models’ unequal ensemble sizes
To assess whether the sampling of one random ensemble member per model from models with unequal ensemble sizes biases the constrained distributions, given the availability of only a single ensemble member from many CMIP6 models, we carry out a synthetic data experiment. The experiment utilizes two sets of synthetic data. We create the first set of data by generating synthetic 50-member ensembles for both the historical predictor and future predictand of each climate model. This process assumes Gaussian distributions for all members of the multi-model ensemble. The Gaussian distributions are centred around the ensemble means of individual models, with the standard deviations obtained from CanESM5. The second dataset is generated using the same approach as the first one, but for each model, the ensemble size corresponds to the actual ensemble size, as listed in Supplementary Table 1. We then compare the constrained PDFs derived from each set of synthetic data using our sampling strategy. The procedure is described in more detail below:
Step 1: construct 50-member synthetic ensembles for observable metrics and projected warming for each model. These ensembles are centred on the respective model means and are sampled from Gaussian distributions with the standard deviations matching those of the CanESM5 large ensemble.
Step 2: randomly select one ensemble member from each of these synthetic 50-member ensembles to generate a PDF of projected warming. Repeat this process 5,000 times, applying the same sampling methodology as described above. The resulting averaged PDF is depicted as the red solid curve in Extended Data Fig. 10.
Step 3: from the 50-member ensembles, select the same number of ensemble members for each model as are actually available, as indicated in Supplementary Table 1. Employ the same sampling method as in step 2 to randomly sample individual ensemble members from this subset and generate an average PDF.
Step 4: repeat step 3 using a different subset of ensemble members. The results are shown with the dashed blue lines in Extended Data Fig. 10.
Our results in Extended Data Fig. 10 show that the distributions obtained using our sampling strategy (dashed blue lines) are similar to the distribution obtained using all available data (red line), suggesting that the limited ensemble sizes available do not have much effect on our resulting PDFs of projected warming.